La mort frappe-t-elle au hasard ?
[Modèle] [Article]

Loup, Lion, Dragon : qui meurt le plus ?
[Modèle] [Article]

Série féministe ou misogyne ?
[Modèle] [Article]

Des corps « masculins et normaux » ?
[Modèle] [Article]

Une cohorte plus à l'abri ?
[Modèle] [Article]

Télécharger en PDF

Pour aller plus loin

=> Télécharger et lire une régression

=> Qualités des modèles

=> Méthodologie régression

Si vous avez les compétences linquistiques de Missandei, aidez-nous à traduire cette page en anglais (ou en valyrien si vous le maîtrisez).

Télécharger et lire une régression

Vous vous sentez un peu perdu ou vous voulez être sûr d'avoir bien compris la lecture des régressions logistiques ? Nous vous offrons ici une lecture détaillée d'un modèle inédit.

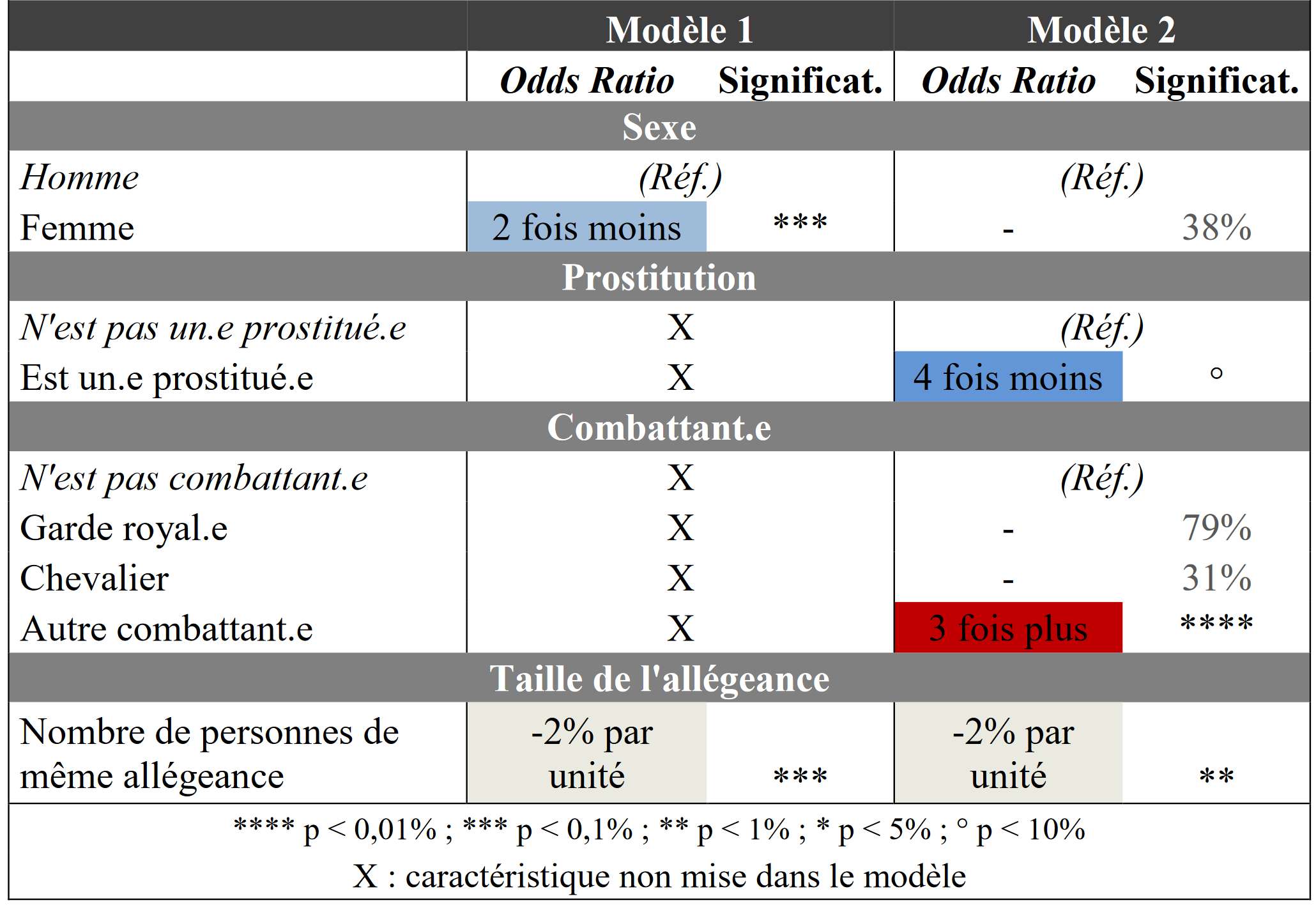
Modèle 1 : nous n'étudions que deux caractéristiques : le sexe du personnage et le nombre de personnages qui appartiennent à la même allégeance que lui. Ainsi, ce premier modèle nous montre qu'à taille d’allégeance égale, les personnages féminins meurent moins que les personnages masculins (Odds Ratio en bleu). Le risque à prendre pour affirmer cela est inférieur à 0,1% (lecture de la significativité - ***) ! Par rapport à un personnage masculin, un personnage féminin a deux fois moins de risque de décéder (lecture de l'Odds Ratio - « 2 fois moins »).

En outre, indépendamment du sexe, chaque personnage supplémentaire au sein d’une allégeance fait diminuer le risque de décès des membres de cette même allégeance de 2% (le risque à prendre pour affirmer l'existance d'un lien entre la taille de l'allégeance et le risque de décès est inférieur à 0,1% - ***).

Mais nous n'avions pas tant besoin d'une régression logistique pour en venir à cette conclusion. En effet, nous savions déjà que, parmi les personnages féminins que nous étudions, 38% décèdent tandis que c'est le cas de 52% des personnages masculins (statistiques descriptives). Le fait de comparer les risques de décès à taille d’allégeance égale n'y change pas grand chose puisque les personnages masculins et féminins appartiennent à des allégeances de taille proches (respectivement 37 et 41 personnages en moyenne).

Modèle 2 : nous pouvons raisonner à structure guerrière et putassière égales. Et cette fois, les effets de composition sont importants ! En effet, les personnages féminins combattent bien moins souvent que leurs homologues masculins (respectivement 17% et 77%). Or, globalement les combattants sont plus exposés : en effet, 68% des combattants décèdent contre seulement 38% des non-combattants - (statistiques descriptives).

De plus, les personnages féminins se prostituent bien plus souvent que leurs homologues masculins (respectivement 15% et 0%). Or, globalement les prostitué.e.s sont moins exposé.e.s : 13% des prostitué.e.s décèdent contre seulement 53% des non-prostitué.e.s - (statistiques descriptives).

En ajoutant ces deux variables au modèle, nous faisons comme si les personnages masculins et les personnages féminins combattaient et se prostituaient autant.

Le fait de combattre expose donc bien à la mort (risque de décès 3 fois plus élevé - lecture de l'Odds Ratio) et être un.e prostitué.e protège bien de la mort (risque de décès 4 fois moins élevé - lecture de l'Odds Ratio). Toutefois, attention, dans le cas de la caractéristique « prostitution », le risque très élevé pour affirmer qu'il existe en effet un lien entre le risque de décéder et le fait de se prostituer. Cela peut paraître étrange compte tenu de la force de Odds Ratio. Mais ceci est dû au fait que très peu de personnages se prostituent et que la robustesse statistique s'en retrouve affectée !

Dans ce second modèle, le risque à prendre pour affirmer qu'il existe des différences de mortalité selon le genre est de 41% : c'est énorme ! C'est pourquoi nous n'affichons pas l'Odds Ratio (cela ne sert à rien de tenter de mesurer l'intensité du lien existant entre le sexe et la mortalité sachant que nous sommes déjà incapables de dire avec un minimum de certitude si cette différence de mortalité). Autrement dit, si les statistiques descriptives faisaient penser que les personnages féminins mourraient moins que les personnages masculins, c'est simplement parce qu’ils occupent des positions qui les protègent. Un personnage féminin qui combat et qui ne se prostitue pas aura les mêmes risques de décès qu'un personnage masculin dans la même situation. Autrement dit : si les personnages masculins et féminins combattaient et se prostituaient autant, ils mourraient probalement autant les uns que les autres.

En conclusion : nous pouvons rassurer les féministes. Il y a bien égalité entre les hommes et les femmes... face à la mort et toutes choses égales par ailleurs…